975. Флойд

Дан ориентированный взвешенный граф. Найдите пару вершин, кратчайшее расстояние от одной из которых до другой максимально среди всех пар вершин.

Вход. В первой строке содержится количество вершин графа n (1 ≤ n ≤ 100). В следующих n строках находится по n чисел, которые задают весовую матрицу графа. В ней -1 означает отсутствие ребра между вершинами, а любое неотрицательное число – присутствие ребра данного веса. На главной диагонали матрицы всегда расположены нули.

Выход. Выведите искомое максимальное кратчайшее расстояние.

Пример входа	Пример выхода
4 0 5 9 -1 -1 0 2 8 -1 -1 0 7 4 -1 -1 0	16

РЕШЕНИЕ

графы – алгоритм Флойда - Уоршела

Анализ алгоритма

В задаче следует реализовать алгоритм Флойда – Уоршела. В ячейках входной матрицы вместо -1 поставим большое натуральное число. Затем в матрице кратчайших расстояний следует найти наибольшее число – оно и будет максимальным кратчайшим расстоянием.

Пример

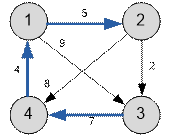
Ниже приведен граф из условия задачи. Максимальное кратчайшее расстояние равно 16 и достигается между вершинами 3 и 2.

Реализация алгоритма

Матрицу смежности графа храним в массиве g. Плюс бесконечность примем равной INF.

#define MAX 101

#define INF 10000000

int g[MAX][MAX];

Функция floyd реализует алгоритм Флойда – Уоршела.

void floyd(void)

{

int i, j, k;

for(k = 0; k < n; k++)

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if (g[i][k] + g[k][j] < g[i][j]) g[i][j] = g[i][k] + g[k][j];

}

Основная часть программы. Читаем входной граф, строим матрицу смежности g.

scanf("%d",&n);

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

scanf("%d",&g[i][j]);

if (g[i][j] < 0) g[i][j] = INF;

}

Запускаем алгоритм Флойда – Уоршела.

floyd();

Находим в переменной res максимальное кратчайшее расстояние между парами вершин.

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if ((g[i][j] > res) && (g[i][j] < INF)) res = g[i][j];

Выводим ответ.

printf("%d\n",res);